Big O

Cheatsheet for Big O Notation.

What is Big O?

Big O notation is a way to describe how long an algorithm takes to run as its input grows. In other words: how quickly its runtime grows relative to the input, as the input gets large. So we can use Big O to compare the performance of algorithms as an input grows and determine the most efficient one. It describes the time complexity of an algorithm. Especially when dealing with sorting algorithms, you'll read a lot about algorithm complexity.

Usually, when we're talking about time complexity, we refer to the worst case complexity. This is the amount of work the algorithm has to do in the worst case scenario. There's also a best case scenario. An example: Let's say you want to check whether an array of numbers includes the number 7. A common approach might be to iterate over all elements and stop when the number was found. You might have luck and the number 7 is at the first index in the array (best case). But it can also be at the last index (worst case), so we have to iterate over all elements.

Instead of time complexity, Big O notation can be also used to describe the space complexity of an algorithm. That refers to the memory occupied by the algorithm.

Keep in mind that Big O describes the efficiency of an algorithm independend of the underlying hardware. Using Big O you can tell which of two algorithms is the more efficient without even running them on a computer. The algorithm complexity may be irrelevant to you when working with a small amount of data, but it's crucial when dealing with large datasets.

Overview

An overview of the most common time complexities. Here, the letter n represents the length of the input array, which can be arbitrarily large.

Big O Complexity (Source)

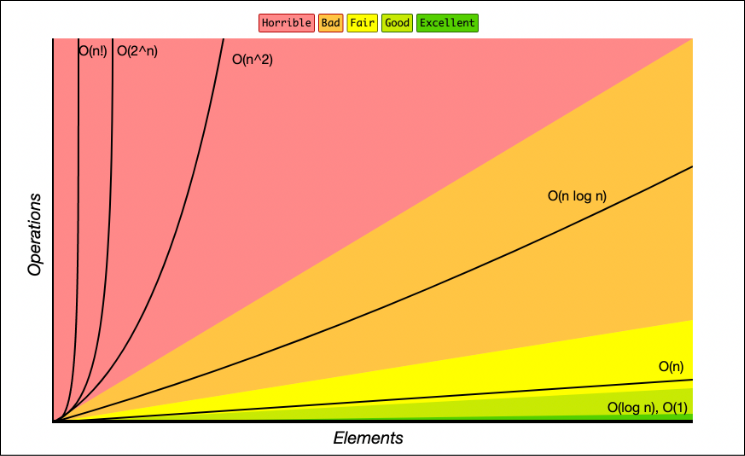
Runtimes

Constant

This method runs in constant time: O(1). Regardless how large the input array is, the runtime remains the same (constant).

def print_first_element(arr):
    print(arr[0])

Linear

This method runs in linear time: O(n). The runtime grows linear to the input array. If the array contains 100 elements, we have to execute 100 prints. For 10.000 elements, we need 10.000 prints and so on.

def print_all_elements(arr):
    for element in arr:
        print(element)

Further Resources

• CS Dojo

• MIT

• AlgoDaily